De ene 1 is de ander niet.

Deze combinatie van beide voorstellingen toont duidelijk de relatieve waarde van een cijfer in een getal.
In het getal 321 heeft de 1 een ander waarde dan in 123.
Leerlingen bij wie dit inzicht ontbreekt maken vaak inversiefouten.
Ze lezen b.v. 84 als 'achtenveertig'.
Dit kan tot ernstige rekenvertraging leiden.
Het is beter de inversiefout te voorkomen.
De scenario's 1 en 2 zijn speciaal met dit doel ontwikkeld.
Accent ligt op het 'groeperen' per 1, per 10 en per 100
De computer laat toe meerdere groeperingsopdrachten af te werken in een
mum van tijd.

Ze laten toe bewerkingen op honderdtallen, tientallen, eenheden... snel voor te stellen.
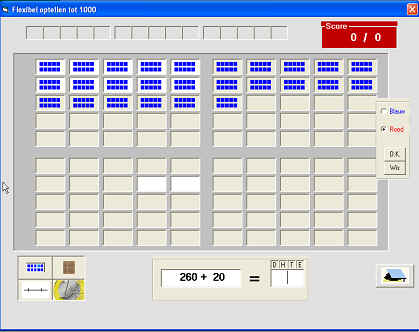
Werken met een gestructureerd duizendveld zoals hierboven afgebeeld is met concreet materiaal zo goed als onmogelijk. Het is nochtans een bijzonder krachtige voorstelling vooral voor rekenzwakke kinderen.
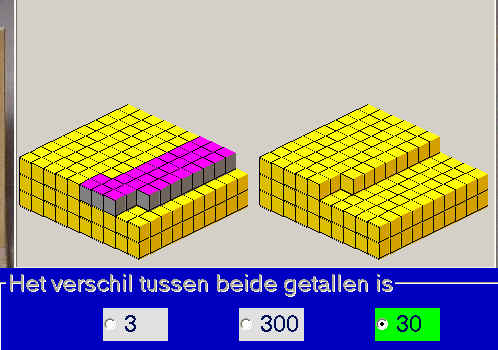
Ook de kubus met duizend blokjes is een krachtig hulpmiddel.
Werken met grote hoeveelheden echte blokjes is niet echt comfortabel.
Een simulatie op de computer kan hetzelfde leereffect hebben...
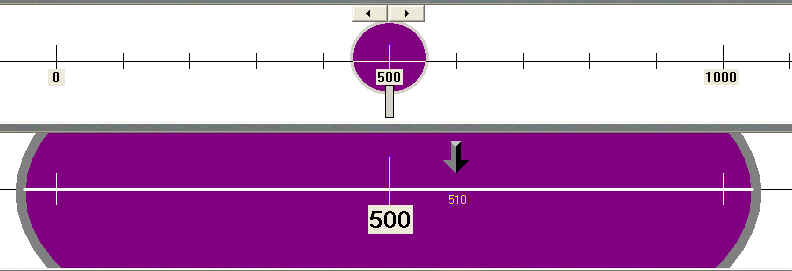
De getallenlijn helpt ons de getallen te ordenen.
Ook hier is de simulatie op de computer grensverleggend o.m. door de inzoommogelijkheden.